I will be continuing in this post about few-shot segmentation, where I will explain the main work we inspired from [4]. I will start to explain the relation between metric learning and softmax classification that was detailed in [4], then further move on explaining the imprinted weights idea.
In points I will explain:
- NCA Proxy Loss (a Metric Learning Method)
- Relation between Metric Learning and Softmax Classification.
- Imprinted Weights
- Relation to other works.
NCA Proxy Loss
Let's start by understanding what is metric learning, these are methods that try to learn a distance function that is consistent with semantic similarity. One category under these is triplet based methods [2] that sample an anchor point, a positive (similar point) and a negative (dissimilar point). The loss defined over these triplets tries to minimize distance between the anchor point and similar ones, while pushing it further form dissimilar ones.
One approach does that by by minimizing the following NCA loss [3] through exponential weighting:
\[L_{NCA}(x, y, Z) = -\log{\frac{\exp{(-d(x, y))}}{\sum_{z \in Z}\exp{(-d(x, z))}} }\]Where \(d\) is the euclidean distance, \(x\) is an anchor point, \(y\) is a positive (similar) data-point and \(Z\) is the set of negative ones. The main problems in triplet based methods generally are: (1) The number of possible triplets from any dataset is huge \(O(n^3)\) (2) You should ensure that you sample meaningful informative triplets. In order to address specifically the later problem some methods use semi-hard negative mining [5]. A recent method [1] tried to solve both problems by trying to learn what they call proxies. Proxies try to approximiate the original data points, and are less than the total number of data points. The method tries to learn these proxies along with the model parameters. One could assign for each class \(c\) a proxy \(p(x) = p_c(x)\) this is called static proxy assignment, and is what we care about in this problem. The NCA loss then becomes:
\[L_{Proxy}(x, p(y), p(Z)) = -\log{\frac{\exp{(-d(x, p(y)))}}{\sum_{p(z) \in p(Z)}\exp{(-d(x, p(z)))}} }\]Where p(x) is the positive proxy and p(z) is the negative proxy. In the case of static proxy assignment we do not sample triplets but rather sample the anchor point and use its positive and negative proxies according to the class label.
Relation between Metric Learning and Softmax Classification
We come at the point where we can see that the above losses resemble a lot what we use to train classification models using softmax cross entropy loss.
\[L_{Proxy}(x, p(y), p(Z)) = -\log{\frac{\exp{(-d(x, p(y)))}}{\sum_{p(z) \in p(Z)}\exp{(-d(x, p(z)))}} }\] \[L_{softmax}(x, c(x)) = -\log{\frac{\exp{(x^Tw_{c(x)})}}{\sum_{c \in C}\exp{(x^Tw_c)}} }\]The main difference between these two loss functions is the use of \(d\) euclidean distance instead of dot product. In case of normalized vectors they are equivelant.
\[\min{(d(x, p(x))} = \max{(x^Tp(x))}\]It is super easy to understand why this happens, following these equations:
\(d(x, p(x)) = ||x - p(x)||_2^2 = (x - p(x))^T(x - p(x))\) \(d(x, p(x)) = x^Tx - 2x^Tp(x) + p(x)^Tp(x) = 2 - 2 x^Tp(x)\)
Note that both \(x^Tx\) is 1 since it is l2 normlaized same for \(p(x)\). We can conclude from the above equations that the weight vector for each class can be looked upon as a proxy itself.
Imprinted Weights
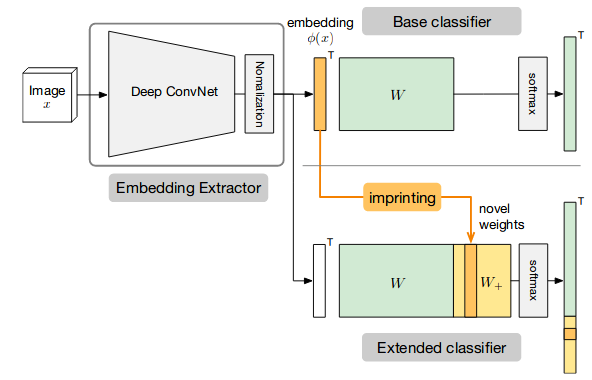
The idea of imprinted weights for few-shot recognition follows from the above relation. You can look to your model as a feature extraction part and a classification layer. If you are trying to learn new classes based on a support set, then you want to learn the new set of weights for these classes. Since from the above we can look to each weight vector per class as a proxy, then you can think of using the l2 normalized embedding vector for the support set as the weight vector itself. This is what is called imprinting according to the work here [4]. The following figure from the paper summarizes the procedure. It starts by training a base network without using meta-training, but in a rather normal training stage and uses a normalization layer to normalize the output embeddings. In the few-shot test phase you can use the support set embeddings averaged per class as your new weight vectors to extend your classifier accordingly.
Relation to Other Works
Whenever I tried to explain the idea I always got the feedback of how this differs from prototypical networks [6]. As far as my understanding the main difference is that prototypical networks will be meta-training the model, it requires to simulate the few-shot setting during the training stage. While this method would directly imprints the weights for the new classes. Prototypical networks is formulated to learn to classify among new classes, and their evaluation setup does not necessarily resemble how we use our vision. We usually know some base classes that we have learned, then we are faced with few samples for new classes that we are required to learn from. In this method it is able to learn to classify among novel and base classes without the need to simulate the few-shot setting.
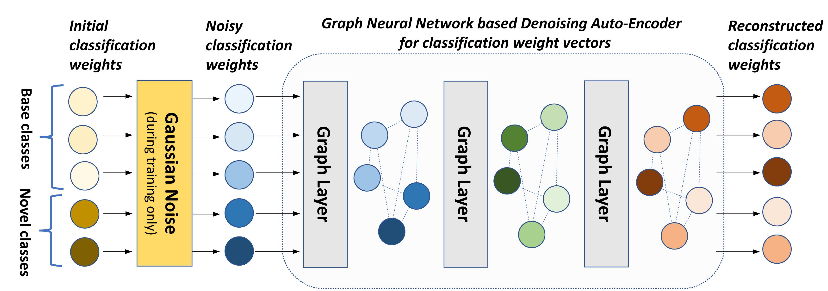
Another interesting related work that uses these imprinted weights as initialization while meta-learning a graph neural network based denoising auto-encoder to improve the weight estimate for both novel and base classes [7]. I am rather just referring to the work for further reading and will not go through explanation as it's out of the scope of explaining what I have built upon.
References
[1] Movshovitz-Attias, Yair, et al. "No fuss distance metric learning using proxies." Proceedings of the IEEE International Conference on Computer Vision. 2017.
[2] Schroff, Florian, Dmitry Kalenichenko, and James Philbin. "Facenet: A unified embedding for face recognition and clustering." Proceedings of the IEEE conference on computer vision and pattern recognition. 2015.
[3] Roweis, Sam, Geoffrey Hinton, and Ruslan Salakhutdinov. "Neighbourhood component analysis." Adv. Neural Inf. Process. Syst.(NIPS) 17 (2004): 513-520.
[4] Qi, Hang, Matthew Brown, and David G. Lowe. "Low-shot learning with imprinted weights." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.
[5] Schroff, Florian, Dmitry Kalenichenko, and James Philbin. "Facenet: A unified embedding for face recognition and clustering." Proceedings of the IEEE conference on computer vision and pattern recognition. 2015..
[6] Snell, Jake, Kevin Swersky, and Richard Zemel. "Prototypical networks for few-shot learning." Advances in Neural Information Processing Systems. 2017.
[7] Gidaris, Spyros, and Nikos Komodakis. "Generating Classification Weights with GNN Denoising Autoencoders for Few-Shot Learning." arXiv preprint arXiv:1905.01102 (2019).
